简化科学的数学探索：用"奥卡姆剃刀"磨砺科学的奥秘

科学的真谛常常隐藏在最简单的解释中，这就是著名的"奥卡姆剃刀"原则。几个世纪以来，这个概念一直在引导着科学的发展，但是当我们面对抽象的概念时，如何辨别它们的价值呢？最近一篇新的研究论文探讨了如何通过比较科学理论的数学基础来评估它们的复杂性，来自加州大学圣巴巴拉分校和加州大学欧文分校的哲学家们领衔探讨。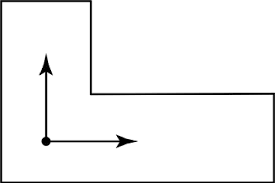



这项研究聚焦于对称性的作用，它强调了利用科学理论的数学结构来衡量复杂性的可能性。虽然对称性不一定能完全决定复杂性，但研究者们发现在理解理论内在结构方面，对称性扮演着重要的角色。这项研究鼓励未来深入探索不同类型的对称性。

通过运用对称性来描述理论结构的数量，也就是在不同变化下保持不变的方面，这是研究者们的目标。经过多次讨论，研究团队开始怀疑对称性是否能够提供所需的框架。然而，他们也揭示了对称性为理解结构提供了卓越的指导。这篇论文发表在《综合》（Synthese）杂志上。

研究的第一作者、加州大学圣巴巴拉分校哲学系副教授托马斯-巴雷特（Thomas Barrett）指出："科学理论通常不会轻易展示自己的解释，因此我们很难理解它们关于世界的真实信息，尤其是对于现代理论。随着时间推移，这些理论变得越来越数学化。而了解不同理论的结构特点，有助于我们深入理解它们所传达的信息，甚至为我们在多个理论中作出选择提供依据。"

研究者们发现，结构不仅可以帮助我们辨别不同观点是否实质上是同一理论，只是表面有所不同。以20世纪初为例，维尔纳-海森堡和埃尔温-薛定谔提出了两种看似截然不同的量子力学理论，然而后来被证明数学上是等价的。

研究一种数学对象常用的方法是研究其对称性。简言之，对称性较强的对象结构较为简单。例如，圆具有无限多的旋转和反射对称性，而箭头则只有一个。这意味着圆相较于箭头来说，更加简单，所需的数学描述也更为简洁。

作者将这一概念推广至更抽象的数学领域。通过比较对象的各个部分，这些函数将它们视为"相似"。这为衡量不同理论结构的复杂性提供了一种启发式方法：理论越复杂，其自身的形式性就越少。

在2012年，两位哲学家提出了一种比较不同理论结构复杂性的方法。只有当数学对象X的自变量是数学对象Y的自变量的子集时，X的结构至少与Y的结构一样多。类比一个半红圆，此法可以用来比较不同结构的复杂性。然而，这个方法过于依赖于物体具有相似类型的对称性，对于更复杂的数学对象则不适用。

新加坡国立大学的艾萨克-威廉试图解决这一敏感性问题。他探索了比较不同类型对称组的可能性，只要能找到它们之间的对应关系，同时保留每个对称组的内部结构。这类变化使得我们能够比较完全不同的数学理论结构，然而也有可能得出错误的结论。巴雷特指出，"不幸的是，威廉的尝试过于激进，不是所有对应关系都能够做到这一点。"

在最新的论文中，研究者们试图通过限制考虑的对称性或自动变形类型来挽救前人的进展。然而，这一尝试也以失败告终。事实上，通过对称性来比较数学结构似乎在原则上注定会失败。例如，考虑一个不对称的物体，如墨迹，尽管存在多种不同的墨迹，它们都完全不同。然而，它们却具有相同的对称性——"无对称性"，这就导致了这些物体被归类为具有相同复杂性的结构，尽管有